MCMCとは

---

ベイズ推定などで、データ $\mathbf{x}$ を与えたうえでの確率分布 $P(\theta |\mathbf{x})$（パラメータ $\theta$ の事後分布）を知りたい場合があります。このような場合、確率変数の状態遷移を記述する マルコフ連鎖 と乱数を用いる モンテカルロ法 を組み合わせた マルコフ連鎖モンテカルロ (MCMC) が有効とされます。MCMCは、$P(\theta |\mathbf{x})$ を直接求めるのではなく、適当な確率分布から繰り返しランダムサンプリングを行うことでマルコフ連鎖を構成し、その収束をもって目的の事後分布を再現する 方法であり、複数のアルゴリズムが提案されています。

マルコフ連鎖

定義

時間ステップ $\{0,1,\dots ,t,t+1,\dots \}$ に対して決まる確率変数列 $\{{\mathbf{X}}_t\}=\{{\mathbf{X}}_1,{\mathbf{X}}_2,\dots \}$ に対して、その観測値を $\{{\mathbf{x}}_t\}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots \}$ とします。このとき、

$$P({\mathbf{x}}_{t+1}|{\mathbf{x}}_t,\dots ,{\mathbf{x}}_1)=P({\mathbf{x}}_{t+1}|{\mathbf{x}}_t)$$

をみたす系列 $\{{\mathbf{x}}_t\}$ は マルコフ連鎖 とよばれます。すなわち、ある時刻での状態は、その直前の状態にのみ依存して決定されることを指します。

---

定常分布

$P({\mathbf{x}}_{t+1}|{\mathbf{x}}_t)$ は 遷移確率（遷移核） とよばれます。いま、状態遷移 $\mathbf{x}\to {\mathbf{x}}^{\prime }$ を考えるとき、

$$P_{\infty }({\mathbf{x}}^{\prime })=\int P({\mathbf{x}}^{\prime }|\mathbf{x})P_{\infty }(\mathbf{x})d\mathbf{x}$$

であるならば分布 $P_{\infty }$ は遷移の前後で変化せず、これを 定常分布 といいます。

---

詳細つり合い条件

定常分布はどんなマルコフ連鎖にも存在するわけではありません。MCMCのキモは、定常分布をもつようなマルコフ連鎖を生成して、収束にもっていくことであるといえます。そのような理由から、マルコフ連鎖が定常分布をもつための条件について考える必要があります。実際にそのような条件は存在して、これを 詳細つり合い条件 といいます：

$$P({\mathbf{x}}^{\prime }|\mathbf{x})P_{\infty }(\mathbf{x})=P(\mathbf{x}|{\mathbf{x}}^{\prime })P_{\infty }({\mathbf{x}}^{\prime })$$

---

メトロポリス法

---

概要

データ $\mathbf{x}$ を与えたうえでのパラメータ $\theta$ の事後分布 $P(\theta |\mathbf{x})$ からサンプリングを行うのがMCMCの目的でした。ベイズの定理を用いれば、

$$P(\theta |\mathbf{x})=\frac{P(\mathbf{x}|\theta )P(\theta )}{\int P(\mathbf{x}|\theta )P(\theta )d\theta }$$

ですが、いま $P(\mathbf{x}|\theta )P(\theta )$（分子）は既知であるとしても、パラメータ空間をなめながらの積分（分母、周辺尤度）が計算できないことを想定します。このような場合には、適当に決めた分布（提案分布）から繰り返しランダムサンプリングを行い、マルコフ連鎖を構成してその定常分布として事後分布 $P(\theta |\mathbf{x})$ を定めます。そのようなアルゴリズムの代表例が メトロポリス法 です。

アルゴリズム

状態遷移 $\mathbf{x}\to {\mathbf{x}}^{\prime }$ について、定常分布 $P_{\infty }(\mathbf{x})$ の確率関数に比例するような $f(\mathbf{x})$ を考えましょう。このとき、詳細つり合い条件が成り立っているとすれば、

$$P({\mathbf{x}}^{\prime }|\mathbf{x})f(\mathbf{x})=P(\mathbf{x}|{\mathbf{x}}^{\prime })f({\mathbf{x}}^{\prime })$$

のように表すことができます。しかしながら、$P(\cdot |\cdot )$ については容易に知ることはできないため、上式をそのまま利用することは困難です。そこで、遷移核として提案分布 $Q(\cdot |\cdot )$ の確率関数 $q(\cdot |\cdot )$ を用います（次の候補 ${\mathbf{x}}^{\prime }$ を $Q(\cdot |\cdot )$ から拾います）。メトロポリス法においては、さらに

$$Q({\mathbf{x}}^{\prime }|\mathbf{x})=Q(\mathbf{x}|{\mathbf{x}}^{\prime })$$

の条件を課し、提案分布は "左右対称" であるとします（例えば、一様分布 $U(-1,1)$ など）。

遷移核を提案分布から求めることによって、詳細つり合い条件の等号は破れてしまいます。そこで、採択率：

$$\alpha =\frac{q(\mathbf{x}|{\mathbf{x}}^{\prime })f({\mathbf{x}}^{\prime })}{q(\mathbf{x}|{\mathbf{x}}^{\prime })f(\mathbf{x})}=\frac{f({\mathbf{x}}^{\prime })}{f(\mathbf{x})}$$

を都度計算し、その結果によって処理を分岐します。具体的には、

$\alpha >1$ のとき：

確率 $\alpha$ で ${\mathbf{x}}^{\prime }$ を採択（${\mathbf{x}}_{t+1}={\mathbf{x}}^{\prime }$）し、$1-\alpha$ で棄却（${\mathbf{x}}_{t+1}=\mathbf{x}$）する。

$\alpha \le 1$ のとき：

確率 $1$ で確定的に ${\mathbf{x}}^{\prime }$ を採択（${\mathbf{x}}_{t+1}={\mathbf{x}}^{\prime }$）する。

というアルゴリズムで列 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots$ を決定します。このような列は、十分な試行回数の下で目標分布 $P_{\infty }(\mathbf{x})$ へ到達します。

Pythonによるメトロポリス法

---

モデル

連続一様分布 $U(-1,1)$ を提案分布とし、2次元正規分布 $N(0,I_2)$ からサンプリングをしてみたいと思います^[1]。

$$f(\mathbf{x})=\exp \left[-\frac{1}{2}{\mathbf{x}}^{\top }\mathbf{x}\right],\mathbf{x}:=(x_1,x_2{)}^{\top }$$

次点の候補 ${\mathbf{x}}^{\prime }$ は、${ϵ}_1,{ϵ}_2\sim U(-1,1)$ なる一様乱数を用いて、

$${\mathbf{x}}^{\prime }:=\mathbf{x}+({ϵ}_1,{ϵ}_2{)}^{\top }$$

と定めます。採択率は、

$$\alpha =\frac{f({\mathbf{x}}^{\prime })}{f(\mathbf{x})}=\exp \left[-\frac{1}{2}({\mathbf{x}}^{\top }\mathbf{x}-{\mathbf{x}}^{\prime \top }{\mathbf{x}}^{\prime })\right]$$

とします。

コーディング

参考コード

Pythonプログラミング（メトロポリス法）

列 ${\mathbf{x}}_t$ は、変数 x1 x2 を保持しながら再代入を繰り返すことで再現します。また、「確率 $\alpha$ で ${\mathbf{x}}^{\prime }$ を採択する」の部分は、 $U(0,1)$ random.uniform(0,1) からランダムに生成した値 p が alpha より大きいか小さいかで判断しています。

また、メトロポリス法の欠点として、提案された候補の採択率が低い（${\mathbf{x}}^{\prime }$ が採択されにくい） ため、特に列の最初では重複を多く含んでしまうことが挙げられます（Burn-in）。この影響を避けるため、5,000回の試行のうち最初の500サンプルは捨てています。

import random
import numpy as np
import matplotlib.pyplot as plt

# destination distribution
def f(x1, x2):
    return np.exp(-0.5 * (x1**2 + x2**2))

# proposal distribution
def q():
    return random.uniform(-1, 1)

# samples
samples = []

# initial value
x1 = 0
x2 = 0
count = 0

# iterations
for i in range(5000):
    # calculate next value
    x1_prime = x1 + q()
    x2_prime = x2 + q()

    # calculate acceptance probability
    alpha = min(1, f(x1_prime, x2_prime) / f(x1, x2))

    # accept or reject
    if (alpha <= 1):
        p = random.uniform(0, 1)
        if (p <= alpha):
            x1 = x1_prime
            x2 = x2_prime
    else:
        x1 = x1_prime
        x2 = x2_prime

    # update count
    count += 1

    # append samples
    if (count > 500):
        samples.append([x1, x2])

# scatter plot
plt.title("Metropolis algorithm")
plt.scatter(list(map(lambda x: x[0], samples)), list(map(lambda x: x[1], samples)), alpha = 0.5)
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.grid(True)
plt.show()

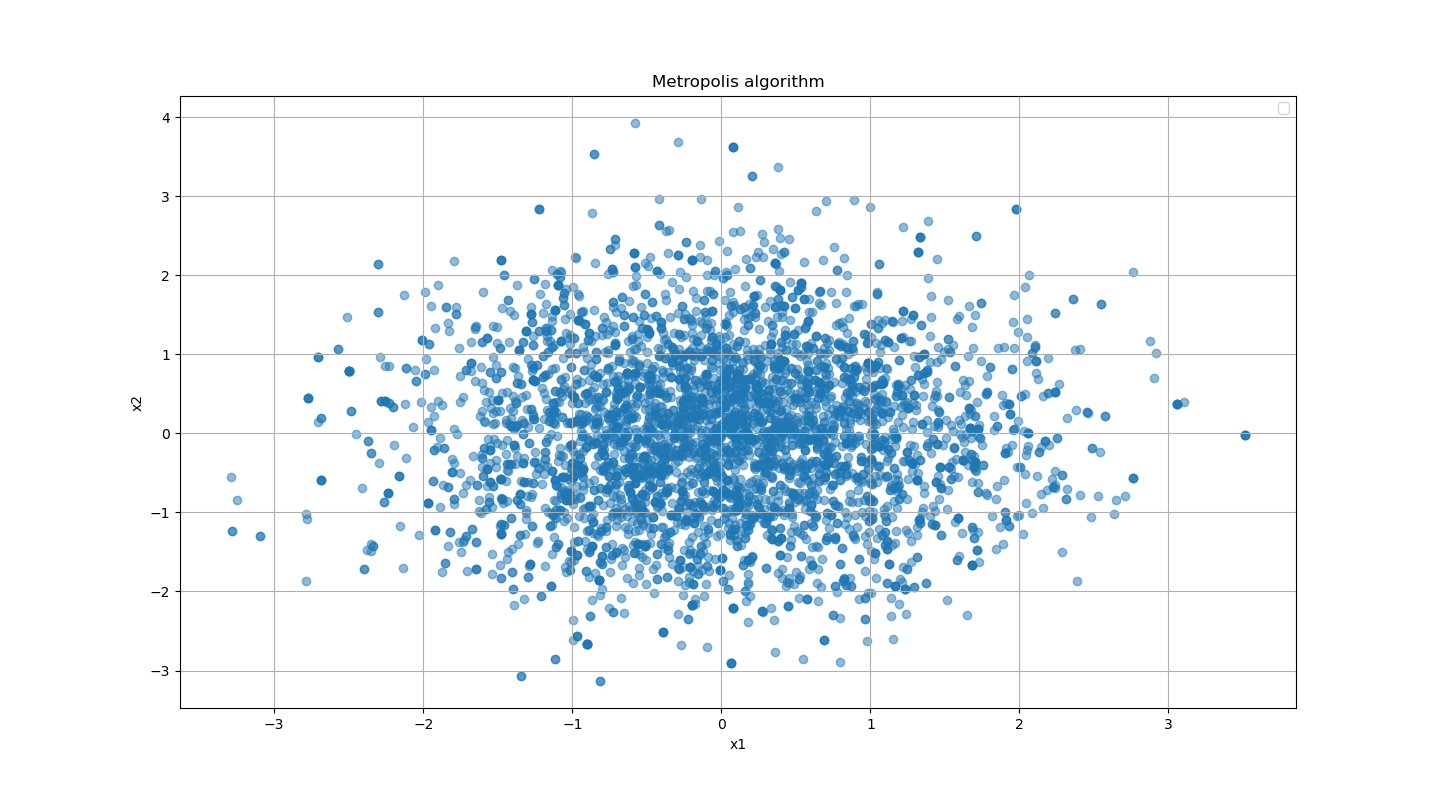
平均 $(0,0)$ を中心に点の密度が高くなっており、2次元正規分布 $N(0,I_2)$ を再現していそうです。

ギブズサンプリング

---

概要

ギブズサンプリング は多次元の分布を推定したい場合に有効です。この方法では、サンプリングしたい事後分布 $P(\theta |x_1,x_2,\dots )$ に対し、条件付き分布：

$$P(x_i|x_1,\dots ,x_{i-1},x_{i+1},\dots )=\frac{P(x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots )}{P(x_1,\dots ,x_{i-1},x_{i+1},\dots )}=\frac{P(x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots )}{\int P(x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots )d{x}_i}$$

を提案分布として次点の候補 $({x_1}^{\prime },{x_2}^{\prime },\dots )$ を決定します。

アルゴリズム

$\mathbf{x}=(x_1,x_2,\dots )$ に対し、次の候補点 ${\mathbf{x}}^{\prime }=({x_1}^{\prime },{x_2}^{\prime },\dots )$ を以下のようにして決めます。

1. ${x_1}^{\prime }$ を $P(x_1|\cdot )$ からサンプリング
2. ${x_2}^{\prime }$ を $P(x_2|\cdot )$ からサンプリング
3. ${x_3}^{\prime }$ を $P(x_3|\cdot )$ からサンプリング
4. 以下、$n$ 次元まで繰り返し

このアルゴリズムが成立するためには、条件付き分布が単純な形で書き表される必要があります^[2]。

Pythonによるギブズサンプリング

---

モデル

2次元正規分布 $N(0,I_2)$ からサンプリングをします。そのために、同時確率関数：

$$f(x_1,x_2)=\frac{1}{\sqrt{(2\pi {)}^2}}\exp \left[-\frac{1}{2}({x_1}^2+{x_2}^2)\right]$$

をもちいて条件付き分布 $f(x_1|x_2)$ を求めます。

$$f(x_1|x_2)=\frac{f(x_1,x_2)}{{\int }_{-\infty }^{\infty }f(x_1,x_2)d{x}_2}=\frac{f(x_1)f(x_2)}{f(x_1)}=f(x_2)$$

対称性から $f(x_2|x_1)=f(x_1)$ でもあります。これらを用いてサンプリングを実行します。

コーディング

この例では条件付き分布が正規分布 $N(0,1)$ であるので、${\mathbf{x}}^{\prime }$ を正規乱数 np.random.standard_normal() としています。また、最初の500サンプルはBurn-inとして破棄しています。

import numpy as np
import matplotlib.pyplot as plt

# samples
samples = []

# initial value
x1 = 0
x2 = 0
count = 0

# iterations
for i in range(5000):
    # calculate next value
    x1_prime = np.random.standard_normal()
    x2_prime = np.random.standard_normal()

    x1 = x1_prime
    x2 = x2_prime

    # update count
    count += 1

    # append sample every 10 counts
    if (count > 500):
        samples.append([x1, x2])

# scatter plot
plt.title("Gibss sampling")
plt.scatter(list(map(lambda x: x[0], samples)), list(map(lambda x: x[1], samples)), alpha = 0.5)
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.grid(True)
plt.show()

こちらも2次元正規分布 $N(0,I_2)$ を再現していそうです。

参考

---

Pythonプログラミング（メトロポリス法）

【MCMC法シリーズその1】MCMC法の概要とメトロポリス法 | note

メトロポリス・ヘイスティング法（マルコフ連鎖モンテカルロ法における手法の一つ）を実装を交えて理解する | Qiita

モンテカルロ法における詳細釣り合い条件と遷移確率の決め方について | Qiita

MCMC入門 Gibbs Sampling

メトロポリス・ヘイスティングス法 | Wikipedia

メトロポリス法 | Wikipedia

脚注

---

1. 一様乱数から正規分布にしたがう乱数を生成する方法としては、変数変換を利用するボックス-ミュラー法が知られています。 ↩︎

2. 例えば、多次元正規分布 $N(\mathbf{\mu },\Sigma )$ の条件付き分布もまた多次元正規分布になることが知られています。 ↩︎