線形単回帰分析について

---

回帰モデル

回帰分析 は，各要因 $X_1,X_2,\dots ,X_n$ がある目的量 $Y$ に対してどの程度影響を与えるかを定量的に見積もる手法です．要因を1つとする場合を単回帰，線形当てはめ（1次式による推定）を行う場合を 線形回帰 といいます．

$$y={\beta }_{1}x+{\beta }_0+u_i$$

傾き ${\beta }_1$ および切片 ${\beta }_0$ は回帰係数で，回帰モデルの特徴を決めます．$u_i$ は誤差項で，通常は正規分布 $N(0,{{\sigma }_u}^2)$ に基づいて揺らぎます．

最小二乗法による回帰係数の推定

導出は省きますが，回帰係数の推定値 ${\hat{\beta }}_1,{\hat{\beta }}_0$ は，データ $(x_i,y_i)$ から計算される基本統計量を用いて次のように表すことができます．

$$\widehat{{\beta }_1}=\frac{S_{xy}}{{S_x}^2}=r_{xy}\frac{S_y}{S_x}$$

$${\hat{\beta }}_0=\bar{y}-{\hat{\beta }}_1\bar{x}$$

ここで $\bar{x},\bar{y}$ は $(x_i,y_i)$ の平均，$S_x,S_y$ は標準偏差（標本分散の平方根），$S_{xy}$ は共分散，$r_{xy}$ は相関係数です．これらを用いて，$x_i$ における予測値 ${\hat{y}}_i$ を次のように計算できます．

$${\hat{y}}_i={\hat{\beta }}_1{x}_i+{\hat{\beta }}_0$$

このとき，回帰係数の推定値から求めた予測値 ${\hat{y}}_i$ と，得られた真の値 $y_i$ との差 $e_i$ を残差といいます．

$$e_i=y_i-{\hat{y}}_i$$

最小二乗法（OLS） とは，この残差の2乗和が最小になるように回帰係数の推定値を定める手法のことです．

$$\mathrm{minimize}\sum _{i=1}^n{e_i}^2$$

このとき，回帰モデルの評価を行うための指標として決定係数 $R^2$ を得ます．決定係数は最大値 $1$ をとり，$1$ に近いほど統計的に有意なモデルであることを表します．

回帰係数のt検定

得られた回帰係数の推定値は有意にゼロと異なるか，すなわち用いた説明変数に説明力があるかを調べるために $t$ 検定を行うことができます．回帰係数（傾き，切片）を ${\beta }_i$，対応する推定値を ${\hat{\beta }}_i$ とし，回帰に用いたデータの数を $n$ とするとき，

$$T=\frac{{\hat{\beta }}_i-{\beta }_i}{\mathrm{SE}({\hat{\beta }}_i)}\sim t(n-2)$$

が成り立ちます．ここで $\mathrm{SE}({\hat{\beta }}_i)$ は ${\hat{\beta }}_i$ の標準誤差で，

$$\mathrm{SE}(\widehat{{\beta }_1})=\sqrt{\frac{\sum _{i=1}^n{e_i}^2}{n-2}\left(\frac{1}{\sum _{i=1}^n(x_i-\bar{x}{)}^2}\right)}$$

$$\mathrm{SE}(\widehat{{\beta }_0})=\sqrt{\frac{\sum _{i=1}^n{e_i}^2}{n-2}\left(\frac{1}{n}+\frac{{\bar{x}}^2}{\sum _{i=1}^n(x_i-\bar{x}{)}^2}\right)}$$

として計算されます．この検定の帰無仮説 $H_0:{\beta }_i=0$，対立仮説 $H_1:{\beta }_i\ne 0$ とし，実際に計算された回帰係数の推定値を $({\hat{\beta }}_i{)}_0$ とすれば，$T$ の実現値 $t$：

$$t=\frac{({\hat{\beta }}_i{)}_0}{\mathrm{SE}(({\hat{\beta }}_i{)}_0)}$$

を得ます．

Rによる線形単回帰分析

---

RStudioのコンソールを用いています。

データのサイズが小さすぎてもつまらないので，より実践的なデータで試してみたいと思います．e-Stat から拾ってきたデータセットから，2021年度における都道府県別の新規大卒者給与（男女平均）と最低賃金の相関を調べてみます．

CSVの編集・読み込み

e-Statから，データセットはCSV形式でダウンロードできます．CSVをVisual Studio Codeで開き，拡張機能のEdit CSVを用いて以下のカラムのみを切り出してみました．これを新しいCSVファイル fetched_payment.csv とします．

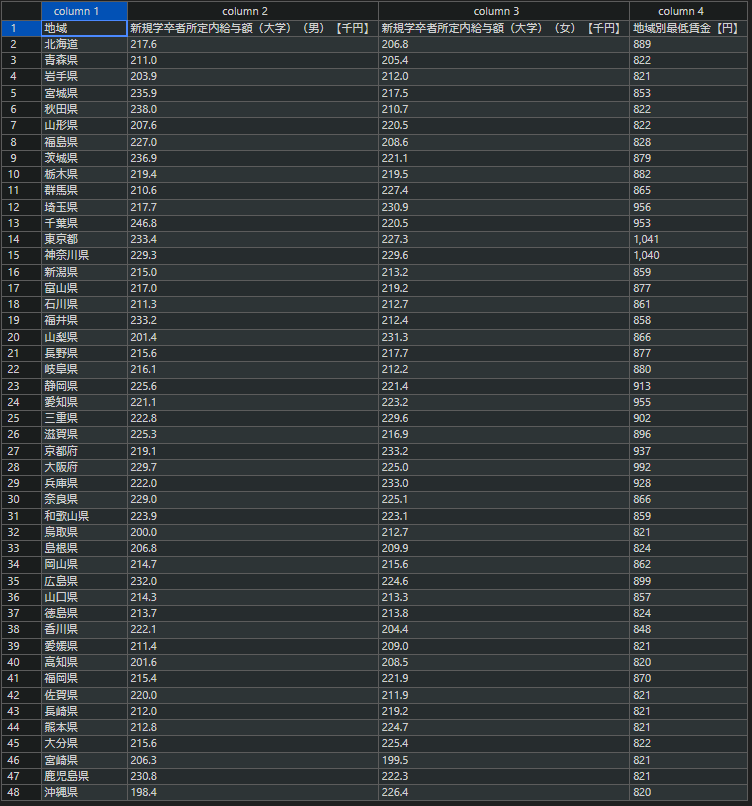
CSVを編集したら，Rの read.csv 関数を用いてデータフレーム df に変換します．このとき，エンコーディングはUTF-8-BOMにするとうまくいきました．

> df <- read.csv("fetched_payment.csv", header = T, fileEncoding = "UTF-8-BOM")

配列操作をする前に，データフレームを行列へ変換してしまいます．as.matrix 関数を使います．

> mat <- as.matrix(df)

説明変数のベクトル（新規大卒者所定内給与）と目的変数のベクトル（最低賃金）を取り出します．ただし，説明変数は男女平均とします．またこのとき，データ型は double とします．as.double 関数でキャストできます．

> x_d <- ( as.double(mat[,2]) + as.double(mat[,3]) ) / 2
> y_d <- as.double(mat[,4])

…どうやらカンマが打たれている数字は double にキャストできないようです．どうにかならんのか（憤怒）

今回はそのようなデータは2件しかないので，仕方なく手入力で復元します．

> y_d[13] <- 1041
> y_d[14] <- 1040

散布図を出力してみます．

> plot(x_d, y_d)

回帰係数の推定値を求める

まずは基本統計量を計算します．ただし標本分散について，Rの関数 var は不偏分散を計算することに注意します．次の関係式を使えばいいでしょう．

$$S^2=\frac{n-1}{n}{U}^2$$

> n <- length(x_d)
> mean_x <- mean(x_d)
> mean_y <- mean(y_d)
> var_x <- ( ( n - 1 ) / n ) * var(x_d)
> var_y <- ( ( n - 1 ) / n ) * var(y_d)
> cov_xy <- cov(x_d, y_d)
> r_xy <- cor(x_d, y_d)

> r_xy
# [1] 0.6636393

相関係数は $0.66$ と計算されました．正の相関がありそうです．

これらから回帰係数の推定値 slope（${\hat{\beta }}_1$）および intercept（${\hat{\beta }}_0$）を求めます．

> slope <- cov_xy / var_x
> slope
# [1] 5.137738

> intercept <- mean_y - slope * mean_x
> intercept
# [1] -251.6389

よって，推定される回帰式は

$$y=5.137738x-251.6389$$

となります．これを散布図上に出力してみましょう．回帰式 $\hat{y}={\hat{\beta }}_{1}x+{\hat{\beta }}_0$ を出力するための関数 hat_y を組み，先ほどの散布図に plot 関数で重ね書きします．add オプションを true に指定していないと上書きされてしまうことに注意します．

> hat_y <- function(x) {
+     return (slope * x + intercept)
+ }
>
> plot(x_d, y_d)   #散布図を消した場合は先に出しておく
> plot(hat_y, min(x_d), max(x_d), add = T)

こんな感じになるでしょうか．それっぽいですね．

t検定を行う

最後に，傾き ${\hat{\beta }}_1$ について $t$ 検定を行っておきましょう．まずは $t$ 値の計算に使う標準誤差を求めます．

> err <- y_d - hat_y(x_d)
> se1 <- sqrt( (sum(err**2)/(n - 2)) * (1/(n * var_x)) )

err は残差です．偏差平方和は標本分散 var_x にサンプルサイズ n をかけて求めます． $t$ 値を計算すると，

> t_val <- slope / se1
> t_val
# [1] 6.079465

となります．帰無仮説 $H_0:{\beta }_1=0$，対立仮説 $H_1:{\beta }_1\ne 0$ ですから，両側検定 となります．有意水準を5%とすると，自由度 $n-2=45$ の $t$ 分布の上側2.5%点は，

> t <- -qt(0.025, df = n - 2)
> t
# [1] 2.014103

と与えられますから，帰無仮説は棄却されます．したがって，有意水準5%で ${\hat{\beta }}_1$ は統計的に意味を持つことがわかります．

この検定を可視化すると以下のようになります．

> curve(dt(x, n - 2), from=-6.5, to=6.5)
> segments(x0 <- seq(t, 6.5, by = 0.02), 0, x0, dt(x0, n - 2))
> segments(x0 <- seq(-6.5, -t, by = 0.02), 0, x0, dt(x0, n - 2))
> abline(v = t_val)

Rの組み込み関数を使う方法

Rには線形回帰（単回帰，重回帰）を行う関数 lm があります．引数には回帰モデル（formula）とデータフレームをとります．

lm(formula, data = data_frame)

要因をincome，目的をwageとし，引数に渡すための新しいデータフレーム df2 を作成します．

> income <- x_d
> wage <- y_d 
>
> df2 <- data.frame(
+     income,
+     wage
+ )

lm 関数で線形単回帰分析を行います．summary 関数で詳細な結果をコンソールに出力することができます．

> result <- lm( wage ~ income, data = df2 )
> summary(result)

Call:
lm(formula = wage ~ income, data = df2)

Residuals:
    Min      1Q  Median      3Q     Max 
-90.461 -30.606   4.056  15.985 113.956 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -227.7280   184.9250  -1.231    0.225    
income         5.0284     0.8449   5.951 3.69e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 42.94 on 45 degrees of freedom
Multiple R-squared:  0.4404,	Adjusted R-squared:  0.428 
F-statistic: 35.42 on 1 and 45 DF,  p-value: 3.689e-07

Coefficients のパートから，回帰式は $y=5.0284x-227.7280$ となったことがわかります．

t value は $5.951$，$P$-値 Pr(>|t|) は $3.7\times 10^{-5}$ であり，${\hat{\beta }}_1$ は有意水準5%で統計的に有意です．

ただし (Intercept) で表される切片 ${\hat{\beta }}_0$ の $P$-値は$0.225$ であり，有意水準5%では統計的に有意であるとは言えません．