ロジスティック回帰モデル

---

定義

ベルヌーイ分布にしたがう確率変数 $Y\sim Bin(1,\theta )$ を応答としてもつ場合を考えます。このとき、2値応答の期待値 $E[Y]=\theta$ を $p$ 個の説明変数 $x_1,x_2,\dots ,x_p$ から推定するモデルとして、ロジスティック回帰モデル：

$$\ln \frac{\theta }{1-\theta }={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p$$

を与えることができます。

シグモイド

簡単のために、ロジスティック単回帰：

$$\ln \frac{\theta }{1-\theta }=\alpha +\beta x$$

を考えます。これを目的変数 $\theta$ について解くと、

$$\theta =\frac{e^{\alpha +\beta x}}{1+e^{\alpha +\beta x}}=\frac{1}{1+e^{-(\alpha +\beta x)}}$$

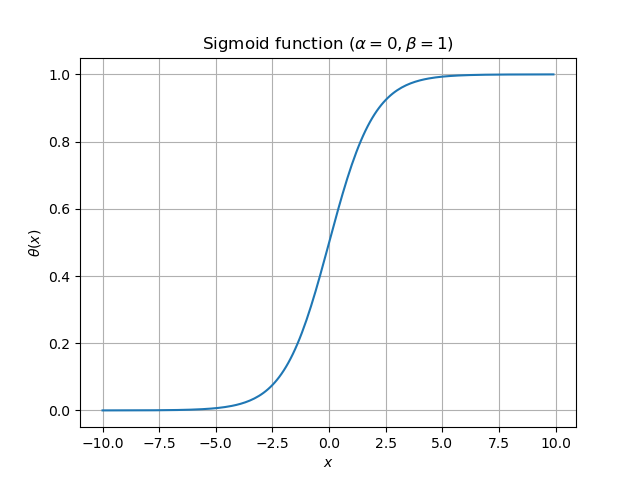
という関数 $\theta (x)$ を得ます。$\alpha ,\beta$ を適当に決めたときのこの関数のグラフを示します：

import numpy as np
import matplotlib.pyplot as plt

# sigmoid function
def theta(x, alpha = 0, beta = 1):
    return 1 / (1 + np.exp(-(alpha + beta * x)))

x = np.arange(-10, 10, 0.1)

plt.plot(x, theta(x))
plt.title(r"Sigmoid function ($\alpha = 0, \beta = 1$)")
plt.xlabel(r"$x$")
plt.ylabel(r"$\theta(x)$")
plt.grid()

plt.show()

以上の関数は2値変数 $\theta \in \{0,1\}$ を実数領域でなめらかに補間した形になっています。このようなS字の関数を シグモイド といいます。

回帰係数の効果

2つの事象が発生する確率の比：

$$\frac{\theta }{1-\theta }=e^{{\beta }_0}\times (e^{{\beta }_1})e^{x_1}\times \cdots \times (e^{{\beta }_p})e^{x_p}$$

を応答 $Y$ の オッズ といい、一方の事象がもう一方の事象に対して何倍程度起こりやすいかを表します。回帰係数 ${\beta }_k$ は、説明変数 $x_k$ がオッズに与える寄与の大きさであることが上式よりわかります。

ロジスティック回帰モデルの最尤推定

---

$p$ 個の説明変数からなるロジスティック回帰モデルにおいて、データ $i=1,2,\dots ,n$ を与えて回帰係数 ${\beta }_0,{\beta }_1,\dots ,{\beta }_p$ を最尤推定することを考えます：

$$\ln \frac{{\theta }_i}{1-{\theta }_i}={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}$$

$i$ 番目の観測値 $x_{i1},x_{i2},\dots ,x_{ip}$ による応答値を $y_i$ とします。このとき、モデルの対数尤度関数は、$i.i.d$ なベルヌーイ分布 $Bin(1,{\theta }_i)$ からの尤度関数を用いて

$$l({\beta }_0,{\beta }_1,\dots ,{\beta }_p)=\ln \left[\prod _{i=1}^n{{\theta }_i}^{y_i}(1-{\theta }_i{)}^{1-y_i}\right]=\sum _{i=1}^n\left[y_i\ln \frac{{\theta }_i}{1-{\theta }_i}+\ln (1-{\theta }_i)\right]$$

と表すことができます。最尤推定量 ${\hat{\beta }}_k$ は $\partial l/\partial {\beta }_k=0$ から求められますが、陽に解くことはできません。最尤推定量 ${\hat{\beta }}_0,{\hat{\beta }}_1,\dots ,{\hat{\beta }}_p$ を用いると、

$$\ln \frac{{\hat{\theta }}_i}{1-{\hat{\theta }}_i}={\hat{\beta }}_0+{\hat{\beta }}_1{x}_{i1}+\cdots +{\hat{\beta }}_p{x}_{ip}$$

が成り立ちますから、$i$ 番目の観測値における生起確率の最尤推定量 ${\hat{\theta }}_i$ は、

$${\hat{\theta }}_i=\frac{1}{1+e^{-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_{i1}+\cdots +{\hat{\beta }}_p{x}_{ip})}}$$

と与えられます。

ポアソン回帰モデル

---

定義

応答 $Y$ が計数値であり、$Y\sim Po(\theta )$ である場合には、その期待値 $E[Y]=\theta$ に対する ポアソン回帰モデル：

$$\ln \theta ={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p$$

を考えることができます。

回帰係数の効果

上式を母数 $\theta$ に対して解くと、

$$\theta =e^{{\beta }_0}\times (e^{{\beta }_1})e^{x_1}\times \cdots \times (e^{{\beta }_p})e^{x_p}$$

です。$\theta$ はポアソン分布の平均であり、めったに起こらない事象の生起回数を表しますから、回帰係数 ${\beta }_k$ は説明変数 $x_k$ が平均 $\theta$ 回起きる事象をどれほど起こりやすくするかの効果を表します。

ポアソン回帰モデルの最尤推定

---

$p$ 個の説明変数からなるポアソン回帰モデルにおいて、データ $i=1,2,\dots ,n$ を与えて回帰係数 ${\beta }_0,{\beta }_1,\dots ,{\beta }_p$ を最尤推定することを考えます：

$$\ln {\theta }_i={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}$$

$i$ 番目の観測値 $x_{i1},x_{i2},\dots ,x_{ip}$ による応答値を $y_i$ とします。このとき、モデルの対数尤度関数は、$i.i.d$ なポアソン分布 $Po({\theta }_i)$ からの尤度関数を用いて

$$l({\beta }_0,{\beta }_1,\dots ,{\beta }_p)=\ln \left[\prod _{i=1}^n{e}^{-{\theta }_i}\frac{{{\theta }_i}^{y_i}}{y_i!}\right]=\sum _{i=1}^n\left[y_i\ln {\theta }_i-\ln y_i!-{\theta }_i\right]$$

と表すことができます。最尤推定量 ${\hat{\beta }}_k$ は $\partial l/\partial {\beta }_k=0$ から求められますが、やはり陽に解くことはできません。

参考

---

書籍

『統計学実践ワークブック』（学術図書出版社, 2020）第18章